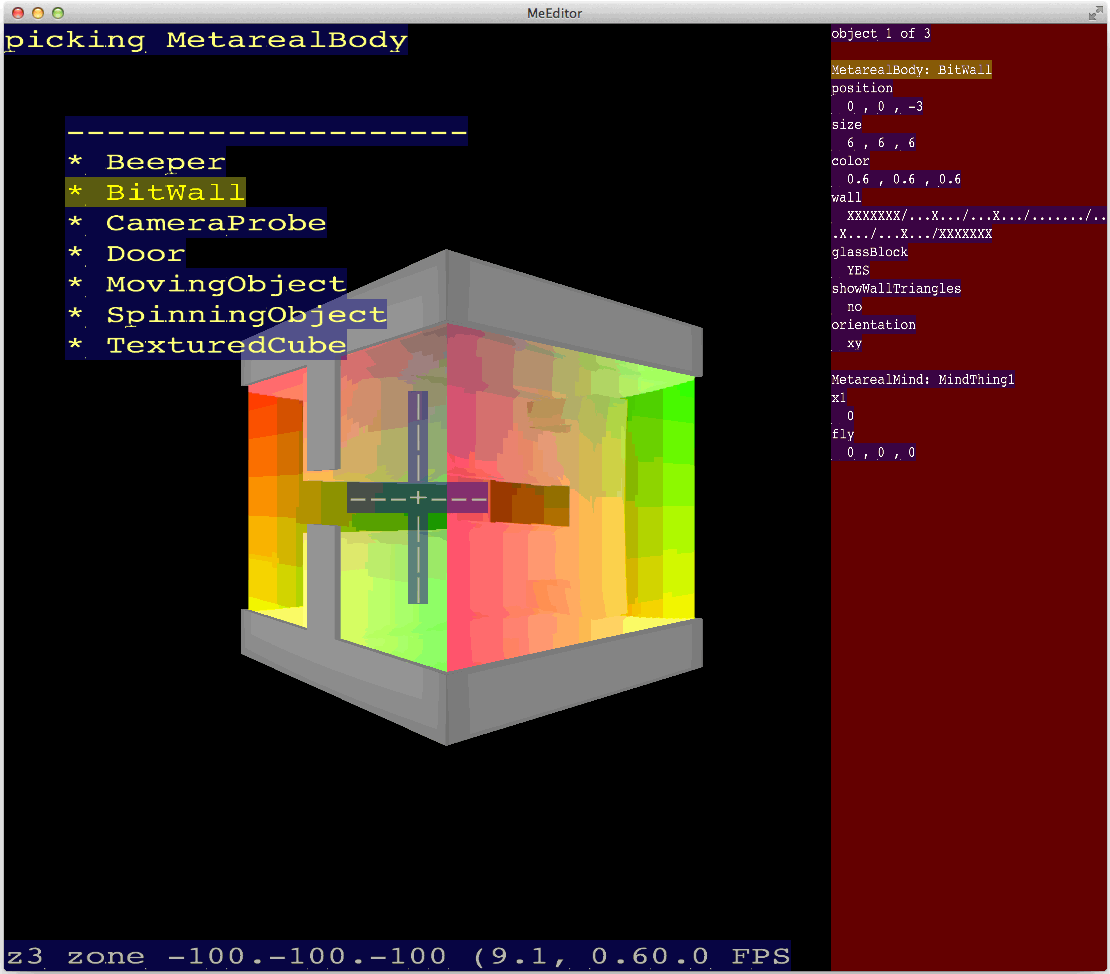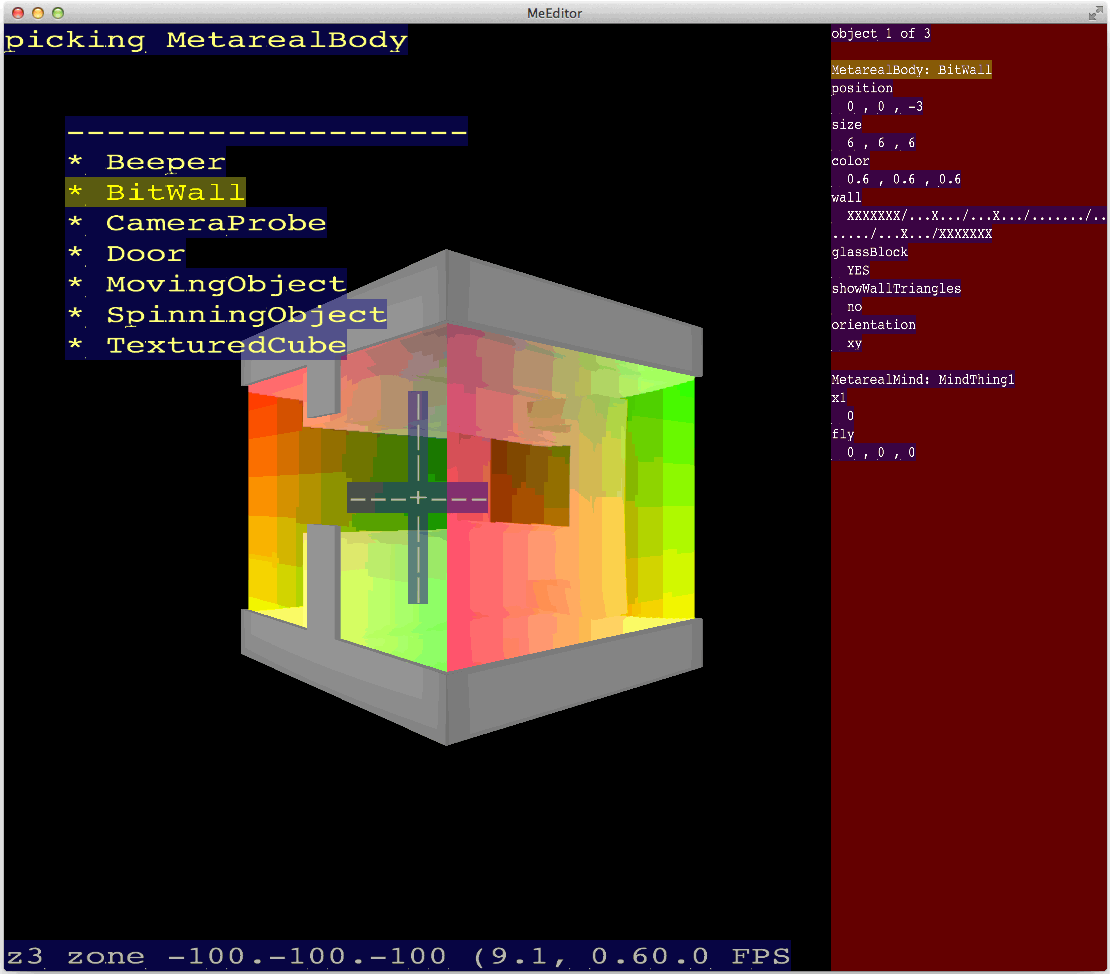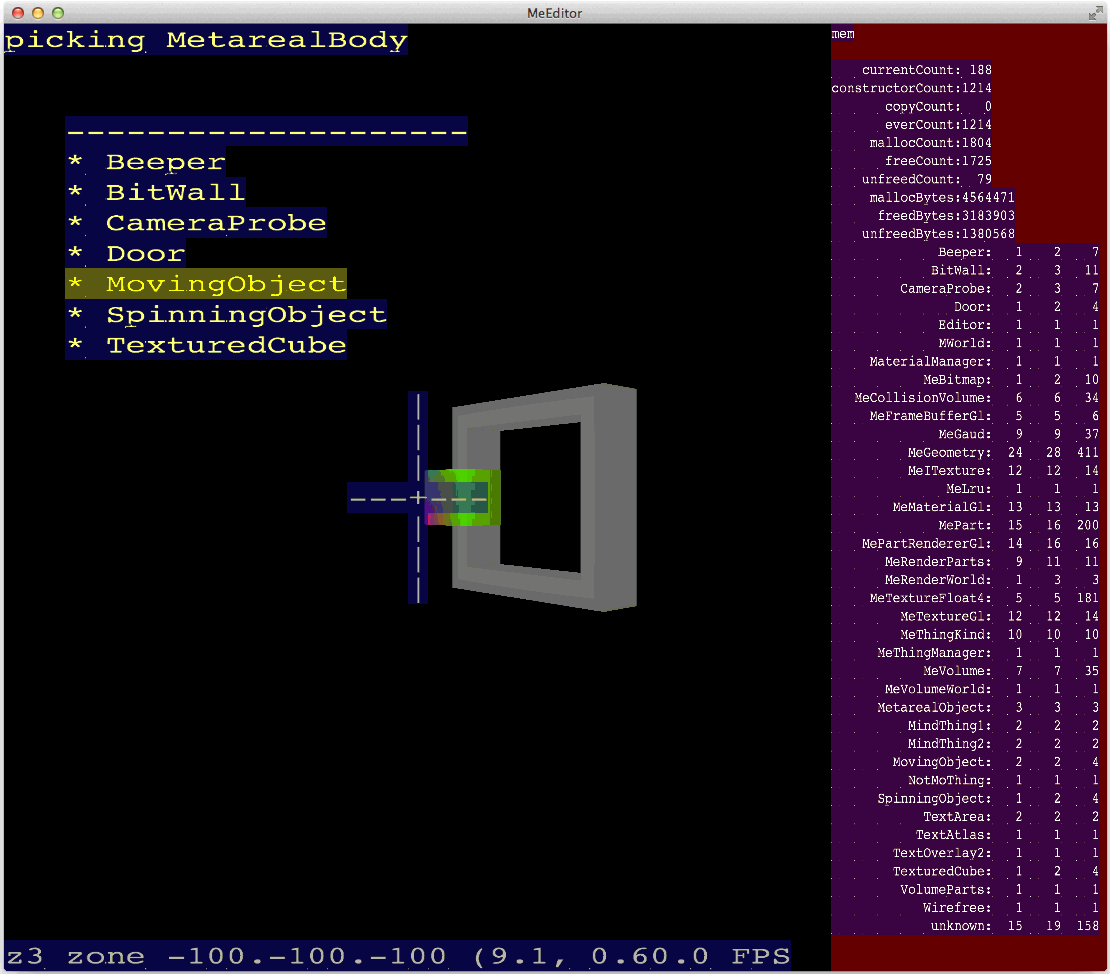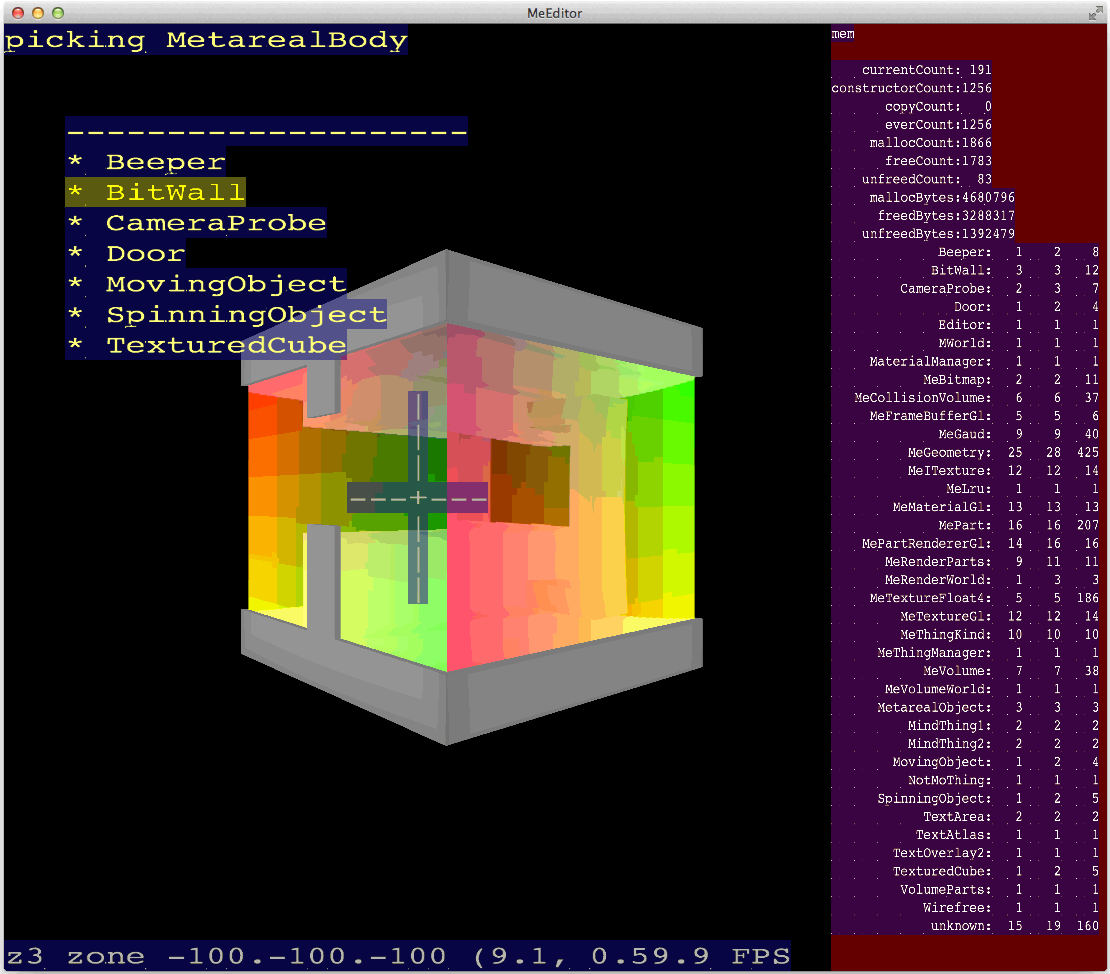
Metareal lets you maneuver unhindered in three dimensional space. There is no gravity, no walking. (And no head-bobbing.) It’s perhaps like a drone moving through a space station.
But I wanted to keep the movement simple and easy. The familiar four-key-and-mouse maneuvering works pretty well, after all.
Problem 1: Nearest Ground Plane
The solution was to treat the mouse relative movements as side-to-side, and up-and-down, relative to the dominant ground plane. It turns out that figuring out which ground plane is best is pretty easy! The camera position and angle can be expressed as a conventional 4×4 column major matrix. From this, we look at the second column, which is where the camera’s Y-Up vector gets mapped to, and see which element has the greatest magnitude. It is that simple!
For example,
/ \ | 0.826 0.070 -0.559 48.700 | | 0.563 -0.103 0.820 -22.325 | | 0.000 -0.992 -0.125 -0.921 | | 0.000 0.000 0.000 1.000 | \ /
We can see for this matrix the bolded value -0.992 shows negative-Z as the dominant Up-vector. So, mouse left and right motions apply, inverted, to the camera’s global Z-rotation. (Arithmetically, we translate the matrix to origin, rotate around global Z, and translate the matrix back to the camera position.)
Problem 2: Don’t go diagonal!

A problem with this approach is you can end up stuck in a “roll”, where, on the new ground plane, you’re not standing upright. Or, rather, you are standing upright, and if you spin left and right the floor stays beneath you, but your head is tilted. To fix this, we need to discover what is our local-Z-rotation relative to the current ground plane. To correct it, we want to rotate the camera along its line of sight, not changing what it is looking at.
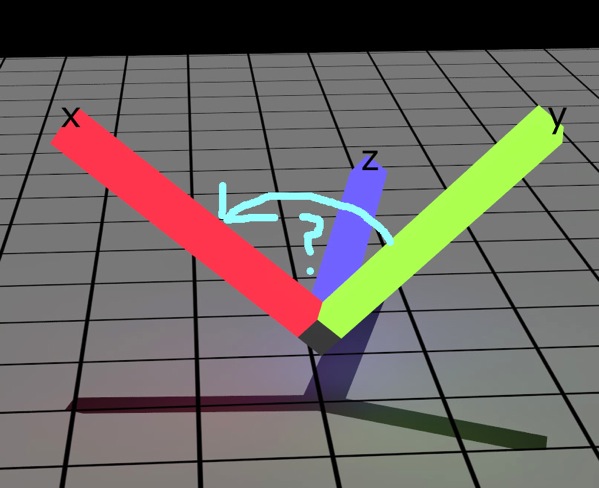
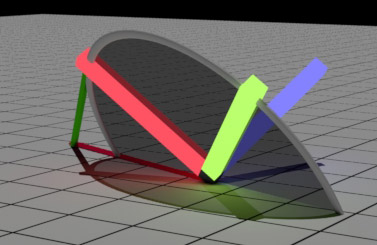
A little vector arithmetic does the trick; we cast the camera’s projected X-axis to the ground plane along the projected Y-axis (up vector), and take the dot product between the X-axis and its line along the ground plane. That’s how much we need to roll. Easy! But how to apply the correction?
Problem 3: Correct The Up-Axis Naturally
I tried three approaches to correcting the up-axis, so that you’re usually looking at square walls and doors and things.
- Manual correction: use some more keyboard keys to roll left and roll right. Terrible! I didn’t like it, anyway.
- Automatic continuous correction: apply some radians-per-second maximum to correcting the roll. It’s ok, but adds a strange smoothness to your image movement sometimes…
- Proportional correction: apply some correction but limited by how much you’re moving the camera yourself. This way the camera never moves except when you’re moving it.
I’m not sure which is best, but I documented all three in a short video.
Also, here’s some code.
float getUpVectorAdjustment()
{
/// for now, just print the angle we suspect...
MeVec3 cameraXVector = this->cameraMatrix.column(0);
MeVec3 cameraYVector = this->cameraMatrix.column(1);
float nope;
int upAxis = axisOf(cameraYVector, &nope);
float t = cameraXVector[upAxis] / cameraYVector[upAxis];
MeVec3 planePoint = cameraXVector - t * cameraYVector;
float thetaDot = cameraXVector.normalize().dot(planePoint.normalize());
thetaDot = pinRangeF(thetaDot, -1, +1); // pin from tiny arithmetic drift...
float theta = acosf(thetaDot);
if(t > 0)
theta = -theta;
return theta;
}