This post is Part 2 of 3 about Metareal’s collision subsystem.

In Part 1, we described the basic, single-axis model of movement, pushing, and blocking. Here we’ll look at more complex movements and collisions, and some special cases.

Diagonal Moves

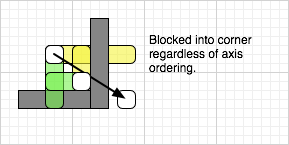
Objects in the Metareal World can move along diagonals. For collision testing, we do this by moving first in X, then Y, and then Z. This can lead to some ambiguities.

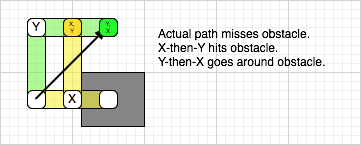
But in practice, most movement is done is smaller steps. This could affect “bullets”, but that doesn’t come up much in Metareal. More importantly, objects can’t escape enclosures such as rooms, regardless of the axis ordering.

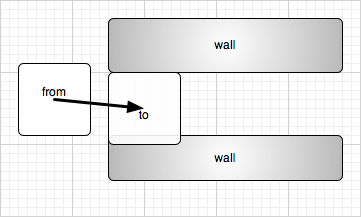
Transporting Into A Bulkhead

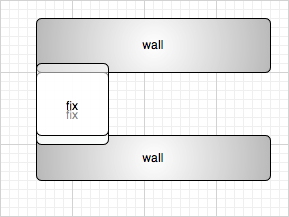
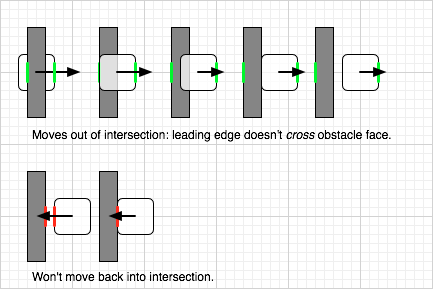
As was mentioned in Star Trek, one of the failure modes for teleportation is materializing inside a bulkhead. Sometimes objects move instantaneously in Metareal. Some doors need to just slam shut, where by “slam” I mean “not slam but rather appear instantly.” But it might do so on top another object, maybe even you! In this case, we allow the object to move out of intersection, and once freed it cannot move back into intersection.

This behavior arises naturally from the process of checking leading edge movements. The leading edge of an object already intersecting an obstacle won’t freshly cross the obstacle face.

The Roundoff Problem

Problem: Due to arithmetic errors, an object that is just barely touching an obstacle sometimes slides right through it.

Consider the following move:

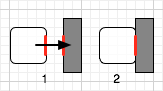
Object moves to the right, stops at the wall. So far, so good. But all these coordinates are floating point. Adding the difference between wall and object to the object’s center, and recomputing the extents introduced a tiny arithmetic error, it’s actually penetrating the wall jussssssst a leedle.

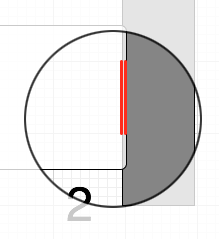
Next time it moves, it can proceed further to the right, satisfying the “ok to move out of collision” rule. But we want it to hit the wall and stop.

Solution: Add a “fudge factor” to the collision distance. The entire Metareal World is about 1200 units across; I’ve found that adding 0.001 to the collision distance brings all roundoff errors back into the positive, not-already-intersecting, realm.

And Part 3 will conclude this series, with a discussion of compound colliders. It’s all made of boxes.

This post is Part 1 of 3 about Metareal’s collision subsystem.

Building my own engine is deeply satisfying. But it is iterative, to be sure. This will be the third major overhaul of the collision system. Might be the last, we’ll see. Where were we…

Move-Then-Fix: A Failed Approach

Back here is a description of a first pass at collision management. Basically, it does these steps:

• Move the thing where the thing thinks it’s going
• Look at any intersections
• Try to do some more movement to get out of intersections
• Some secret sauce to move the least, but also not get snagged on seams, and stuff like that

It worked just enough to fool me. But had problems. Here’s one. When moving into a narrow space, but more “into” than “across”:

The minimal intersection-fix is also illegal, and would lead to a metastable vibration:

In some cases it’d just get stuck in walls. Maybe with further analysis it could undo more of the move, but it’s no longer so simple as “Move and then fix.” It also didn’t support “pushing” in any obvious way. So came up with a whole new approach.

Recursive Intersection Testing

When an object A moves distance d in the X-axis, one of four things will happen:

1. It will move the entire distance without bumping into anything
2. It will bump into something it cannot push, and stop
3. It will bump into object B that it can push, and might continue pushing it

In case 3, then object B must be tested for however far A might push it. This is implemented recursively. And it is performed independently for each axis of motion.

Here’s an example. A moves 4 units to the right, so it’s going to bump into B and C. Also, B will hit a wall.

The analysis descends like so:

• A wants to move 4 units right. How far can you move, A?
• A sees intersections first with C (1 unit away) and then B (2 units away)
• Recurse. C wants to move 3 units right. How far can you move, C?
• C has no intersections within 3 units. I can move all 3 units!
• Recurse. B wants to move 2 units right. How far can you move, B?
• B hits a wall in 1 unit. I can move 1 unit right.
• We know that A can move 3 units to the right (distance to B is 2, plus how far B can move).

After this analysis, we simply move A 3 units right, and each of the previously analyzed intersections moves by what’s left.

And this is done for delta X, delta Y, and delta Z. Doing these axes separately completely eliminates any possibility of entering a shaft too narrow for the object.

The Bullet Problem

Problem: If an object is moving quickly, its proposed position could be on the other side of a wall, with no intersection.

Solution: Move only the leading edge. That is, check for intersections of the swept volume.

The actual test is simply: Does the leading edge start out before the closest edge of the obstacle, and end after the obstacle. In the implementation there’s plenty of cruft relating to positive- or negative-motion, to check which edges are moved, which are compared against, and so on.

That’s enough for this post. Part 2 will discuss diagonal movement and roundoff errors. Part 3 will describe collision objects more complex than “A Box”.